Queries for Standard tableaux: search statistic / browse statistics / browse maps from / browse maps to
Definition & Example
-
A standard (Young) tableau of a partition $\lambda \vdash n $ is a bijection between $\{1,2,\dots, n\}$ and the cells (also known as boxes) of the Young diagram of $\lambda$, such that rows and columns are increasing.
-
The set of standard tableaux of size $n$ is denoted by $\mathcal{SYT}_n$ where the size is given by the size of the underlying partition $\lambda \vdash n$.
| the 4 Standard tableaux of size 3 | |||
 |
 |
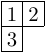 |
 |
| [[1,2,3]] | [[1,3],[2]] | [[1,2],[3]] | [[1],[2],[3]] |
- Standard tableaux are graphically represented by filling the cells of the Young diagram in English notation.
Properties
-
The number of standard tableaux of a partition $\lambda$ is given by the well known hook-length formula
$$ \big|\mathcal{SYT}_\lambda\big| = \frac{n!}{\prod hook(B)},$$where the product ranges over all boxes $B$ in the Young diagram of $\lambda$, and where $hook(B)$ is the hook length of $B$ in $\lambda$. The hook length of $B$ is the number of boxes in the same row to the right of $B$, plus the number of boxes in the same column below $B$ plus the box itself. -
The number of standard tableaux of size $n$ cells is counted by the involution numbers, with the first few terms (beginning with $n=0$) being 1, 1, 2, 4, 10, 26.
Remarks
- The number of standard tableaux of shape $(n,n)$ is counted by the $n^{th}$ Catalan number, $\operatorname{C}_n = \frac{1}{n+1} \binom{2n}{n}$.
- There is a bijection between permutations $ \pi \in \mathbf{S}_n $ and pairs $(P,Q)$ of Standard Tableaux of shape $\lambda \vdash n $, known as the Robinson--Schensted correspondence. Furthermore, the length of the longest increasing subsequence of $\pi$ is equal to the length of the first row of $P$ (or $Q$), and the length of the longest decreasing subsequence of $\pi$ is equal to the height of the first column of $P$. [Sch61]
- There is a bijection between Standard Young Tableaux of shape $(3×n)$ and irreducible webs for ${sl_3}$ whose boundary vertices are all sources [Tym12]
References
- [Sch61] C. Schensted, Longest increasing and decreasing subsequences, Canad. J. Math. 13(1961), 179-191
- [Tym12] Julianna Tymoczko, A simple bijection between standard 3×n tableaux and irreducible webs for sl3, J Algebr Comb (2012) 35:611–632
Sage examples
Technical information for database usage
- A standard tableau is uniquely represented as a list of lists giving the fillings of the cells row by row.
- Standard tableaux are graded by the size.
- The database contains all standard tableaux of size at most 8.
If you want to edit this wiki page, you can download the raw markdown and send your new version to info@findstat.org