Queries for Alternating sign matrices: search statistic / browse statistics / browse maps from / browse maps to
Definition & Example
- An alternating sign matrix (ASM) of order $n$ is an $n \times n$-matrix with entries $-1$, $0$ or $+1$ such that the sum of the entries in each row and each column equals $1$ and the nonzero entries alternate in sign along each row and each column.
| the 7 Alternating sign matrices of size 3 | ||||||
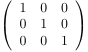 |
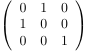 |
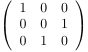 |
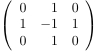 |
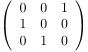 |
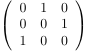 |
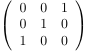 |
| [[1,0,0],[0,1,0],[0,0,1]] | [[0,1,0],[1,0,0],[0,0,1]] | [[1,0,0],[0,0,1],[0,1,0]] | [[0,1,0],[1,-1,1],[0,1,0]] | [[0,0,1],[1,0,0],[0,1,0]] | [[0,1,0],[0,0,1],[1,0,0]] | [[0,0,1],[0,1,0],[1,0,0]] |
- There are $\displaystyle M(n):=\prod_{i=0}^{n-1}\frac{(3i+1)!}{(n+i)!}$ ASMs of order $n$, see A005130.
Properties
-
Every permutation matrix is an ASM.
-
There is exactly one $1$ in the first row of an ASM. Zeilberger [Zei96b] proved that the number of ASMs of order $n$ whose unique $1$ of the first row is in the $r$th column is given by $\displaystyle \frac{\binom{n+r-2}{n-1} \binom{2n-1-r}{n-1}}{\binom{3n-2}{n-1}} \prod_{i=0}^{n-1}\frac{(3i+1)!}{(n+i)!}$. See [Beh13] for a more refined enumeration of ASMs.
-
There are eight symmetry classes of ASMs. Except for the cases of diagonally symmetric ASMs, totally symmetric ASMs, and diagonally and antidiagonally symmetric ASMs of even order, there are proven product formulae for the straight enumeration in all classes, see [Rob91], [Rob], [BFK17] .
-
There is a bijective correspondence between ASMs and monotone triangles. Monotone triangles of order $n$ are Gelfand-Tsetlin patterns with strictly decreasing rows and top row $n,n-1,\dots,1$.
-
ASMs are in bijection with fully-packed loop configurations (FPL). The enumeration problem of FPLs with a given link pattern has only been solved for certain link patterns. Razumov and Stroganov conjectured a relation between the enumeration of FPLs with a given link pattern and the dense $O(1)$-loop model. It was proved combinatorially by Cantini and Sportiello [CS11].
-
There is a bijective correpsondence between ASMs and the six-vertex model with domain wall boundary conditions.
-
Domino tilings of Aztec diamonds correspond to the so-called $2$-enumeration of ASMs [EKLP92a], [EKLP92b].
Remarks
-
The notion of ASMs arose in Robbins' and Rumsey's study of $\lambda$-determinants in the early 1980s [RR86]. They conjectured with Mills the enumeration formula for ASMs [MRR83], which had been known as the alternating sign matrix conjecture before being independently proved to hold true by Zeilberger [Zei96a], Kuperberg [Kup96], and Fischer [Fis16]. See [BP99] for more information about the history of the alternating sign matrix conjecture.
-
$M(n)$ enumerates several other objects: descending plane partitions whose parts do not exceed $n$ [MRR83], [And79]; totally symmetric self-complementary plane partitions inside a $2n \times 2n \times 2n$-box [MRR86], [And94]; alternating sign triangles with $n$ rows [ABF]. However, no bijections between these objects and ASMs have been found so far.
References
- [ABF] A. Ayyer, R. E. Behrend, I. Fischer, Extreme diagonally and antidiagonally symmetric alternating sign matrices of odd order, preprint arXiv:1611.03823 [math.CO ]
- [And79] G. E. Andrews, Plane partitions (III): The weak Macdonald conjecture, Inventiones mathematicae 53.3 (1979)
- [And94] G. E. Andrews, Plane Partitions V: The TSSCPP Conjecture, Journal of Combinatorial Theory, Series A 66.1 (1994)
- [BFK17] R. E. Behrend, I. Fischer, M. Konvalinka, Diagonally and antidiagonally symmetric alternating sign matrices of odd order, Advances in Mathematics 315 (2017)
- [BP99] D. Bressoud, J. Propp, How the alternating sign matrix conjecture was solved, Notices of the AMS 46.6 (1999)
- [Beh13] R. E. Behrend, Multiply-refined enumeration of alternating sign matrices, Advances in Mathematics 245 (2013)
- [CS11] L. Cantini, A. Sportiello, Proof of the Razumov–Stroganov conjecture, Journal of Combinatorial Theory, Series A 118.5 (2011)
- [EKLP92a] N. Elkies, G. Kuperberg, M. Larsen, J. Propp, Alternating-sign matrices and domino tilings (Part I), Journal of Algebraic Combinatorics 1.2 (1992)
- [EKLP92b] N. Elkies, G. Kuperberg, M. Larsen, J. Propp, Alternating-sign matrices and domino tilings (Part II), Journal of Algebraic Combinatorics 1.3 (1992)
- [Fis16] I. Fischer, Short proof of the ASM theorem avoiding the six-vertex model, Journal of Combinatorial Theory, Series A 144 (2016)
- [Kup96] G. Kuperberg, Another proof of the alternative-sign matrix conjecture, International Mathematics Research Notices 1996.3 (1996)
- [MRR83] W. H. Mills, D. P. Robbins, H. Rumsey, Alternating sign matrices and descending plane partitions, Journal of Combinatorial Theory, Series A 34.3 (1983)
- [MRR86] W. H. Mills, D. P. Robbins, H. Rumsey, Self-complementary totally symmetric plane partitions, Journal of Combinatorial Theory, Series A 42.2 (1986)
- [RR86] D. P. Robbins, H. Rumsey, Determinants and alternating sign matrices, Advances in Mathematics 62.2 (1986)
- [Rob] D. P. Robbins, Symmetry classes of alternating sign matrices, preprint arXiv:math/0008045 [math.CO ]
- [Rob91] D. P. Robbins, The Story of 1, 2, 7, 42, 7436,..., The Mathematical Intelligencer 13.2 (1991)
- [Zei96a] D. Zeilberger, Proof of the alternating sign matrix conjecture, Electronic Journal of Combinatorics 3 (1996), R13
- [Zei96b] D. Zeilberger, Proof of the refined alternating sign matrix conjecture, New York Journal of Mathematics 2 (1996)
Sage examples
Technical information for database usage
- An alternating sign matrix is uniquely represented as a list of lists representing its rows.
- Alternating sign matrices are graded by its size.
- The database contains all alternating sign matrices of size at most 6.