Queries for Dyck paths: search statistic / browse statistics / browse maps from / browse maps to
Definition & Example
- A Dyck path of semilength $n$ is a lattice path from $(0,0)$ to $(2n,0)$ consisting of $n$ up steps of the form $(1,1)$ and $n$ down steps of the form $(-1,1)$ which never goes below the x-axis $y=0$. Denote all Dyck paths of size $n$ by $\mathfrak{D}_n$.
Equivalently, a Dyck path of semilength $n$ can be seen as
-
a lattice path from $(0,0)$ to $(n,n)$ consisting of $n$ up steps of the form $(1,0)$ and $n$ down steps of the form $(0,1)$ which never goes below the diagonal $y=x$.
-
a Dyck word, this is a word in $\{0,1\}$ such that any prefix contains at least as many $1$'s as it contains $0$'s. Seeing a $1$ as an opening bracket and a $0$ as a closing bracket, Dyck words can be seen as well-formed bracketing systems.
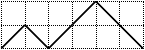
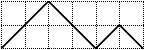
| the 5 Dyck paths of size 3 | ||||
 |
 |
 |
 |
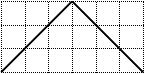 |
| [1,0,1,0,1,0] | [1,0,1,1,0,0] | [1,1,0,0,1,0] | [1,1,0,1,0,0] | [1,1,1,0,0,0] |
- There are $\operatorname{Cat}(n) = \frac{1}{n+1}\binom{2n}{n}$ Dyck paths of semilength $n$, see OEIS:A000108. This can for example be seen using the reflection principle.
Properties
-
A Dyck path $D$ of size $n+1$ can be decomposed into a Dyck path $D_1$ of size $k$ and a Dyck path $D_2$ of size $n-k$, where
-
$(2k+2,0)$ is the first touch point of $D$ at the x-axis,
-
$D_1$ is the prefix of $D$ from $(1,1)$ to $(2k-1,1)$ never going below the line $y=1$, and where
-
$D_2$ is the suffix of $D$ from $(2k,0)$ to $(2n,0)$.
This yields the recurrence
Remarks
-
There is a natural extension of Dyck paths to $m$-Dyck paths which can be seen as lattice paths from $(0,0)$ to $(mn,n)$ that never go below the diagonal $y = \frac{1}{m} x$. The number of $m$-Dyck paths is given by the Fuss-Catalan number $C^{(m)}(n) = \frac{1}{mn+1} \binom{(m+1)n}{n}$ [Kra89].
-
Dyck paths and $m$-Dyck paths can be seen as type A instances of a more general combinatorial object for root systems, namely positive chambers in the (generalized) Shi arrangement [Ath04].
-
Dyck paths of semilength $n$ are in canonical bijection with Nakayama algebras with linear quiver and $n+1$ simple modules.
References
- [Ath04] C.A. Athanasiadis, Generalized Catalan numbers, Weyl groups and arrangements of hyperplanes, Bull. London Math. Soc., 36 (2004), pp. 294-392
- [Kra89] C. Krattenthaler, Counting lattice paths with a linear boundary II, Sitz.ber. d. ÖAW Math.-naturwiss. Klasse 198 (1989), 171-199
Sage examples
Technical information for database usage
- A Dyck path is uniquely represented as a Dyck word.
- Dyck paths are graded by the semilength.
- The database contains all Dyck paths of semilength at most 8.