Queries for Permutations: search statistic / browse statistics / browse maps from / browse maps to
Definition & Example
- A permutation of size $n$ is a bijection of $\{1,\ldots,n\}$. $\mathfrak{S}_n$ denotes the set of all such permutations.
There are two standard ways to denote $\pi \in \mathfrak{S}_n$.
- The one-line notation is given by $\pi = [\pi(1),\ldots,\pi(n)]$. E.g., $\pi = [5,4,2,3,1]$ says that
- The cycle notation is given by $\pi = (a^{(1)}_1, \ldots, a^{(1)}_{k_1}) \cdots (a^{(m)}_1, \ldots, a^{(m)}_{k_m})$ which means that every integer in a cycle is mapped to the next integer in this cycle, $\pi(a^{(j)}_i) = a^{(j)}_{i+1}$. E.g., $$\pi = (1,5)(2,4,3) = [5,4,2,3,1].$$Often, fixed points are suppressed in the cycle notation.
| the 6 Permutations of size 3 | |||||
| [1,2,3] | [1,3,2] | [2,1,3] | [2,3,1] | [3,1,2] | [3,2,1] |
- There are $n! = 1\cdot 2 \cdot 3 \cdots n$ permutations of size $n$, see A000142.
Additional information
The Rothe diagram of a permutation
- A way to visualize a permutation is by drawing its Rothe diagram introduced by H.A. Rothe in 1800. It is given by the collection of boxes $$R(\sigma) = \{ (\sigma_j,i) : i < j, \sigma_i > \sigma_j \}.$$Alternatively, $R(\sigma)$ is by marking all boxes $b_i = (i,\sigma_i)$ and cross out all boxes below and to the right of $b_i$.
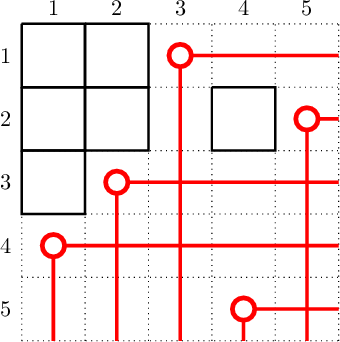 |
- The essential set of the Rothe diagram is the collection of boxes $(i,j)$ for which $(i+1,j)$ and $(i,j+1)$ are both not in the Rothe diagram. The Rothe diagram can also be used to understand the Bruhat order on permutations, see [Man01]. It is also closely related to the Lehmer code for a permutation, described below.
Euler-Mahonian statistics
L. Carlitz proved in [Car54] that the generating function for the bistatistic $(\operatorname{des},\operatorname{maj})$ satisfies a nice recurrence: let
A permutation statistic is called
- Eulerian if it is equidistributed with the number of descents (St000021),
- Mahonian if it is equidistributed with the major index (St000004), and
- Euler-Mahonian if it is equidistributed with the bistatistic $(\operatorname{des},\operatorname{maj})$, see e.g. [FZ94].
Two additional examples of Euler-Mahonian statistics are
- the bistatistic $(\operatorname{exc},\operatorname{den})$ given by the number of exceedences (St000155) and the Denert index (St000156), see [FZ90],
- the bistatistic $(\operatorname{stc},\operatorname{inv})$ given by the number of sub-stairs and the number of inversions (St000018), see [Ska01].
The Lehmer code and the major code of a permutation
-
The Lehmer code encodes the inversions (St000018) of a permutation. It is given by $L(\sigma) = l_1 \ldots l_n$ with $l_i = \# \{ j > i : \sigma_j < \sigma_i \}$. In particular, $l_i$ is the number of boxes in the $i$-th column of the Rothe diagram. The Lehmer code of $\sigma = [4,3,1,5,2]$ is for example given by $32010$. The Lehmer code $L : \mathfrak{S}_n\ \tilde\longrightarrow\ S_n$ is a bijection between permutations of size $n$ and sequences $l_1\ldots l_n \in \mathbf{N}^n$ with $l_i \leq i$.
-
The major code $M(\sigma)$ of a permutation $\sigma \in \mathfrak{S}_n$ is, similarly to the [../#The Lehmer code for a permutation Lehmer code], a way to encode a permutation as a sequence $m_1 m_2 \ldots m_n$ with $m_i \geq i$. To define $m_i$, let $\operatorname{del}_i(\sigma)$ be the normalized permutation obtained by removing all $\sigma_j < i$ from the one-line notation of $\sigma$. The $i$-th index is then given by
Special classes of permutations
Pattern-avoiding permutations
-
A permutation $\sigma$ avoids a permutation $\tau$ if no subword of $\sigma$ in one-line notation appears in the same relative order as $\tau$. E.g. $[4,2,1,3]$ is not $[3,1,2]$-avoiding since the subword $[4,1,3]$ has the same relative order as $[3,1,2]$. See also the wiki page on permutation pattern and the references therein. Each subword of $\sigma$ having the same relative order as $\tau$ is called occurrence of $\tau$.
-
Is was proven in [Knu68] that $3$-pattern avoiding permutations are all counted by the famous Catalan numbers,
-
A permutation $\sigma$ avoids a pattern $ab\!\!-\!\!c$ for $\{a,b,c\} = \{1,2,3\}$ if it avoids the permutation $[a,b,c]$ with the additional property that the positions of $a$ and $b$ in $\sigma$ must be consecutive. In other words, a pattern $ab\!\!-\!\!c$ in $\sigma$ is a subword $\sigma_i,\sigma_{i+1},\sigma_j$ with $\sigma_i > \sigma_j > \sigma_{i+1}$. In particular, usual three-pattern-avoidance is of the form $a\!\!-\!\!b\!\!-\!\!c$.
-
Mesh patterns, introduced by [BrCl11], constitute a further generalization. A mesh pattern is a pair $(\tau, R)$, where $\tau\in\mathfrak{S}_k$ and $R$ is a subset of $\{0,\dots,k\}\times\{0,\dots,k\}$. An occurrence of $(\tau, R)$ in a permutation $\pi$ is an occurrence $(t_1,\dots,t_k)$ of $\tau$ in $\pi$, satisfying the following additional requirement: for all $(i,j)\in R$, the permutation $\sigma$ has no values between $t_j$ and $t_{j+1}$ in the positions between the positions of $t_i$ and $t_{i+1}$, where we set $t_0=0$ and $t_k=n+1$.
Thus, classical patterns are mesh patterns with empty $R$ and vincular patterns are mesh patterns with a shaded column.
Classes of permutations in Schubert calculus
The following classes of permutations play important roles in the theory of Schubert polynomials, see e.g. [Man01, Section 2.2]. A permutation $\sigma \in \mathfrak{S}_n$ is called
- dominant if the following equivalent conditions hold:
- its Lehmer code is a partition, this is if $l_1 \geq l_2 \geq \ldots \geq l_n$,
- its Rothe diagram is the shape of a partition. In particular, $\sigma$ is dominant if and only if $\sigma^{-1}$ is dominant.
- it is $[1,3,2]$ avoiding. The Schubert polynomial $S_\sigma(x,y)$ for a dominant permutation $\sigma$ is given by $S_\sigma(x,y) = \prod_{(i,j) \in \lambda(\sigma)} (x_i - y_j),$ where $\lambda(\sigma)$ is the shape of the Rothe diagram of $\sigma$ [Man01, Proposition 2.6.7].
- Grassmannian if the following equivalent conditions hold:
- $l_1 \leq l_2 \leq \ldots \leq l_r$ and $l_i = 0$ for for some $r$ and all $i>r$,
- $\sigma$ has a unique descent (St000021). The Schubert polynomial $S_\sigma(x)$ for a Grassmannian permutation $\sigma$ is given by $S_\sigma(x) = s_{\lambda(\sigma)}(x_1,\ldots,x_n)$, where $s_\lambda$ is the Schur function for the shape $\lambda$ [Man01, Proposition 2.6.8].
- bigrassmannian if $\sigma$ and $\sigma^{-1}$ are both Grassmannian.
Bigrassmannian permutations can be used to describe the Bruhat order on permutations: $\sigma \leq \tau$ in Bruhat order if and only if every bigrassmannian permutation dominated by $\sigma$ is also dominated by $\tau$ [LS96].
- vexillary if the following equivalent conditions hold:
- its Rothe diagram is, up to a permutation of its rows and columns, the diagram of a partition,
- there is no sequence $i < j < k < l$ with $\sigma_j < \sigma_i < \sigma_l < \sigma_k$,
- its essential set lies on a piecewise linear curve oriented $SW-NE$. The Schubert polynomials for vexillary permutations are exactly the flagged Schur functions, see [Man01, Section 2.6.5] for a detailed description. The term vexillary comes from the Latin vexillum for a flag-like object used in the Classical Era of the Roman Empire [Man01, p. 65] and is due to A. Lascoux and M.-P. Schützenberger.
Properties
- The cycle type of a permutation $\pi \in \mathfrak{S}_n$ is given by the integer partition of $n$ formed by the lengths of the cycles of $\pi$. E.g., $\pi = (1,4,3,7)(2)(5,6)$ has cycle type $[4,2,1]$. Two permutations $\pi$ and $\tau$ in $\mathfrak{S}_n$ are conjugated (i.e., $\pi = \sigma \tau \sigma^{-1}$ for some $\sigma \in \mathfrak{S}_n$) if and only if their cycle types coincide.
Remarks
-
The symmetric group is a Coxeter group and a finite reflection group.
-
The symmetric group admits a beautiful representation theory.
References
- [BrCl11] P. Brändén and A. Claesson, Electron. J. Combin, 2011
- [Car54] L. Carlitz, q-Bernoulli and Eulerian numbers, Trans. Amer. Math. Soc. 76 (1954), p. 332-350
- [FZ90] D. Foata, D. Zeilberger, Denert’s permutation statistic is indeed Euler-Mahonian, Studies in Appl. Math. 83 (1990)
- [FZ94] , ,
- [Knu68] D. Knuth, The Art Of Computer Programming Vol. 1, Boston: Addison-Wesley (1968)
- [LS96] A. Lascoux, M.-P. Schützenberger, Treillis et bases des groupes de Coxeter, Electron. J. Combin. 3(2) (1996)
- [Man01] L. Manivel, Symmetric functions, Schubert polynomials and degeneracy loci, SMF/AMS Texts and Monographs 6 (2001)
- [Ska01] M. Skandera, An Eulerian partner for inversions, Sém. Loth. Comb. 46 (2001)
Sage examples
Technical information for database usage
- Permutations are graded by size.
- The database contains all permutations of size at most 7.