Queries for Permutations: search statistic / browse statistics / browse maps from / browse maps to

Definition & Example

A permutation of size $n$ is a bijection of $\{1,\ldots,n\}$. $\mathfrak{S}_n$ denotes the set of all such permutations.

There are two standard ways to denote $\pi \in \mathfrak{S}_n$.

The one-line notation is given by $\pi = [\pi(1),\ldots,\pi(n)]$. E.g., $\pi = [5,4,2,3,1]$ says that

$$\pi(1)=5,\pi(2)=4,\pi(3)=2,\pi(4)=3,\pi(5)=1.$$

The cycle notation is given by $\pi = (a^{(1)}_1, \ldots, a^{(1)}_{k_1}) \cdots (a^{(m)}_1, \ldots, a^{(m)}_{k_m})$ which means that every integer in a cycle is mapped to the next integer in this cycle, $\pi(a^{(j)}_i) = a^{(j)}_{i+1}$. E.g.,
$$\pi = (1,5)(2,4,3) = [5,4,2,3,1].$$
Often, fixed points are suppressed in the cycle notation.

the 6 Permutations of size 3
`[1,2,3]`	`[1,3,2]`	`[2,1,3]`	`[2,3,1]`	`[3,1,2]`	`[3,2,1]`

There are $n! = 1\cdot 2 \cdot 3 \cdots n$ permutations of size $n$, see A000142.

Additional information

The Rothe diagram of a permutation

A way to visualize a permutation is by drawing its Rothe diagram introduced by H.A. Rothe in 1800. It is given by the collection of boxes
$$R(\sigma) = \{ (\sigma_j,i) : i < j, \sigma_i > \sigma_j \}.$$
Alternatively, $R(\sigma)$ is by marking all boxes $b_i = (i,\sigma_i)$ and cross out all boxes below and to the right of $b_i$.

	The Rothe diagram of $\sigma = [4,3,1,5,2]$

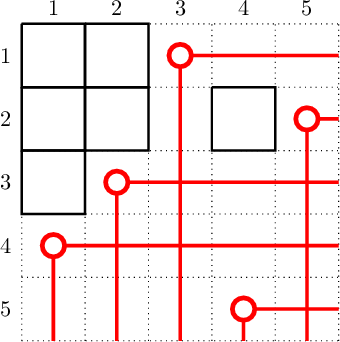The essential set of the Rothe diagram is the collection of boxes $(i,j)$ for which $(i+1,j)$ and $(i,j+1)$ are both not in the Rothe diagram. The Rothe diagram can also be used to understand the Bruhat order on permutations, see [Man01]. It is also closely related to the Lehmer code for a permutation, described below.

Euler-Mahonian statistics

L. Carlitz proved in [Car54] that the generating function for the bistatistic $(\operatorname{des},\operatorname{maj})$ satisfies a nice recurrence: let

$$B_n(q,t) = \sum_{\sigma \in \mathbf{S}_n} t^{\operatorname{des}(\sigma)} q^{\operatorname{maj}(\sigma)} = \sum_{k=0}^n B_{n,k}(q) t^k.$$

Then the coefficient $B_{n,k}(q)$ satisfy the recurrence

$$B_{n,k}(q) = [k+1]_q B_{n-1,k}(q) + q^k[n-k]_q B_{n-1,k-1}(q), \qquad B_{0,k}(q) = \delta_{0,k}.$$

A permutation statistic is called

Eulerian if it is equidistributed with the number of descents (St000021),
Mahonian if it is equidistributed with the major index (St000004), and
Euler-Mahonian if it is equidistributed with the bistatistic $(\operatorname{des},\operatorname{maj})$, see e.g. [FZ94].

Two additional examples of Euler-Mahonian statistics are

the bistatistic $(\operatorname{exc},\operatorname{den})$ given by the number of exceedences (St000155) and the Denert index (St000156), see [FZ90],
the bistatistic $(\operatorname{stc},\operatorname{inv})$ given by the number of sub-stairs and the number of inversions (St000018), see [Ska01].

The Lehmer code and the major code of a permutation

The Lehmer code encodes the inversions (St000018) of a permutation. It is given by $L(\sigma) = l_1 \ldots l_n$ with $l_i = \# \{ j > i : \sigma_j < \sigma_i \}$. In particular, $l_i$ is the number of boxes in the $i$-th column of the Rothe diagram. The Lehmer code of $\sigma = [4,3,1,5,2]$ is for example given by $32010$. The Lehmer code $L : \mathfrak{S}_n\ \tilde\longrightarrow\ S_n$ is a bijection between permutations of size $n$ and sequences $l_1\ldots l_n \in \mathbf{N}^n$ with $l_i \leq i$.
The major code $M(\sigma)$ of a permutation $\sigma \in \mathfrak{S}_n$ is, similarly to the [../#The Lehmer code for a permutation Lehmer code], a way to encode a permutation as a sequence $m_1 m_2 \ldots m_n$ with $m_i \geq i$. To define $m_i$, let $\operatorname{del}_i(\sigma)$ be the normalized permutation obtained by removing all $\sigma_j < i$ from the one-line notation of $\sigma$. The $i$-th index is then given by

$$m_i = \operatorname{maj}(\operatorname{del}_i(\sigma)) - \operatorname{maj}(\operatorname{del}_{i-1}(\sigma)).$$

For example, the permutation $[9,3,5,7,2,1,4,6,8]$ has major code $[5, 0, 1, 0, 1, 2, 0, 1, 0]$ since

$$\operatorname{maj}([8,2,4,6,1,3,5,7]) = 5, \quad \operatorname{maj}([7,1,3,5,2,4,6]) = 5, \quad \operatorname{maj}([6,2,4,1,3,5]) = 4,$$

$$\operatorname{maj}([5,1,3,2,4]) = 4, \quad \operatorname{maj}([4,2,1,3]) = 3, \quad \operatorname{maj}([3,1,2]) = 1, \quad \operatorname{maj}([2,1]) = 1.$$

Observe that the sum of the major code of $\sigma$ equals the major index of $\sigma$.

Special classes of permutations

Pattern-avoiding permutations

A permutation $\sigma$ avoids a permutation $\tau$ if no subword of $\sigma$ in one-line notation appears in the same relative order as $\tau$. E.g. $[4,2,1,3]$ is not $[3,1,2]$-avoiding since the subword $[4,1,3]$ has the same relative order as $[3,1,2]$. See also the wiki page on permutation pattern and the references therein. Each subword of $\sigma$ having the same relative order as $\tau$ is called occurrence of $\tau$.
Is was proven in [Knu68] that $3$-pattern avoiding permutations are all counted by the famous Catalan numbers,

$$ \#\big\{ \sigma \in \mathfrak{S}_n : \sigma \text{ avoids } \tau \big\} = \frac{1}{n+1}\binom{2n}{n}, $$

where $\tau$ is any permutation in $\mathfrak{S}_3$.

A permutation $\sigma$ avoids a pattern $ab\!\!-\!\!c$ for $\{a,b,c\} = \{1,2,3\}$ if it avoids the permutation $[a,b,c]$ with the additional property that the positions of $a$ and $b$ in $\sigma$ must be consecutive. In other words, a pattern $ab\!\!-\!\!c$ in $\sigma$ is a subword $\sigma_i,\sigma_{i+1},\sigma_j$ with $\sigma_i > \sigma_j > \sigma_{i+1}$. In particular, usual three-pattern-avoidance is of the form $a\!\!-\!\!b\!\!-\!\!c$.
Mesh patterns, introduced by [BrCl11], constitute a further generalization. A mesh pattern is a pair $(\tau, R)$, where $\tau\in\mathfrak{S}_k$ and $R$ is a subset of $\{0,\dots,k\}\times\{0,\dots,k\}$. An occurrence of $(\tau, R)$ in a permutation $\pi$ is an occurrence $(t_1,\dots,t_k)$ of $\tau$ in $\pi$, satisfying the following additional requirement: for all $(i,j)\in R$, the permutation $\sigma$ has no values between $t_j$ and $t_{j+1}$ in the positions between the positions of $t_i$ and $t_{i+1}$, where we set $t_0=0$ and $t_k=n+1$.

Thus, classical patterns are mesh patterns with empty $R$ and vincular patterns are mesh patterns with a shaded column.

Classes of permutations in Schubert calculus

The following classes of permutations play important roles in the theory of Schubert polynomials, see e.g. [Man01, Section 2.2]. A permutation $\sigma \in \mathfrak{S}_n$ is called

dominant if the following equivalent conditions hold:
- its Lehmer code is a partition, this is if $l_1 \geq l_2 \geq \ldots \geq l_n$,
- its Rothe diagram is the shape of a partition. In particular, $\sigma$ is dominant if and only if $\sigma^{-1}$ is dominant.
- it is $[1,3,2]$ avoiding. The Schubert polynomial $S_\sigma(x,y)$ for a dominant permutation $\sigma$ is given by $S_\sigma(x,y) = \prod_{(i,j) \in \lambda(\sigma)} (x_i - y_j),$ where $\lambda(\sigma)$ is the shape of the Rothe diagram of $\sigma$ [Man01, Proposition 2.6.7].
Grassmannian if the following equivalent conditions hold:
- $l_1 \leq l_2 \leq \ldots \leq l_r$ and $l_i = 0$ for for some $r$ and all $i>r$,
- $\sigma$ has a unique descent (St000021). The Schubert polynomial $S_\sigma(x)$ for a Grassmannian permutation $\sigma$ is given by $S_\sigma(x) = s_{\lambda(\sigma)}(x_1,\ldots,x_n)$, where $s_\lambda$ is the Schur function for the shape $\lambda$ [Man01, Proposition 2.6.8].
bigrassmannian if $\sigma$ and $\sigma^{-1}$ are both Grassmannian.

Bigrassmannian permutations can be used to describe the Bruhat order on permutations: $\sigma \leq \tau$ in Bruhat order if and only if every bigrassmannian permutation dominated by $\sigma$ is also dominated by $\tau$ [LS96].

vexillary if the following equivalent conditions hold:
- its Rothe diagram is, up to a permutation of its rows and columns, the diagram of a partition,
- there is no sequence $i < j < k < l$ with $\sigma_j < \sigma_i < \sigma_l < \sigma_k$,
- its essential set lies on a piecewise linear curve oriented $SW-NE$. The Schubert polynomials for vexillary permutations are exactly the flagged Schur functions, see [Man01, Section 2.6.5] for a detailed description. The term vexillary comes from the Latin vexillum for a flag-like object used in the Classical Era of the Roman Empire [Man01, p. 65] and is due to A. Lascoux and M.-P. Schützenberger.

Properties

The cycle type of a permutation $\pi \in \mathfrak{S}_n$ is given by the integer partition of $n$ formed by the lengths of the cycles of $\pi$. E.g., $\pi = (1,4,3,7)(2)(5,6)$ has cycle type $[4,2,1]$. Two permutations $\pi$ and $\tau$ in $\mathfrak{S}_n$ are conjugated (i.e., $\pi = \sigma \tau \sigma^{-1}$ for some $\sigma \in \mathfrak{S}_n$) if and only if their cycle types coincide.

Remarks

The symmetric group is a Coxeter group and a finite reflection group.
The symmetric group admits a beautiful representation theory.

References

[BrCl11] P. Brändén and A. Claesson, Electron. J. Combin, 2011
[Car54] L. Carlitz, q-Bernoulli and Eulerian numbers, Trans. Amer. Math. Soc. 76 (1954), p. 332-350
[FZ90] D. Foata, D. Zeilberger, Denert’s permutation statistic is indeed Euler-Mahonian, Studies in Appl. Math. 83 (1990)
[FZ94] , ,
[Knu68] D. Knuth, The Art Of Computer Programming Vol. 1, Boston: Addison-Wesley (1968)
[LS96] A. Lascoux, M.-P. Schützenberger, Treillis et bases des groupes de Coxeter, Electron. J. Combin. 3(2) (1996)
[Man01] L. Manivel, Symmetric functions, Schubert polynomials and degeneracy loci, SMF/AMS Texts and Monographs 6 (2001)
[Ska01] M. Skandera, An Eulerian partner for inversions, Sém. Loth. Comb. 46 (2001)

Sage examples

Technical information for database usage

Permutations are graded by size.
The database contains all permutations of size at most 7.

If you want to edit this wiki page, you can download the raw markdown and send your new version to info@findstat.org